https://pnpsumml.tistory.com/4
[DL] Activation Functions Insight ~ 활성화 함수의 발전과 통찰 -1-
이 글에서는 활성화 함수 중 대표적인 것들을 살펴보고, 그 발전에 있던 insight들을 이해하며 활성화 함수의 역할과 이를 위한 특성을 이해해보려고 한다. 딥 러닝 모델에 있어 활성화 함수는 다
pnpsumml.tistory.com
1부 글에서 계단 함수부터 시작하여 ReLU에 이르기까지, 특히 ReLU의 특성에 집중하며 그 발전 과정과 그 발전을 불러온 문제점과 통찰을 살펴보았다.


대표적으로 음의 구간에서 작은 양의 기울기를 가져 음의 활성화 값을 보전하는 Leaky ReLU와, 여기에 지수 함수를 이용해 음의 구간 활성화 값이 발산하지 않도록 하는 SELU(Scaled Exponential Linear Unit) 등 수많은 접근과 그에 따른 개선판이 등장했다.
그러나 어떤 점을 개선하면서, 어떤 부분은 의미론적으로 변조가 되기도 했다. 예를 들어 ReLU가 음의 구간에서 칼같이 음의 활성화 값을 차단하여 보았던 성능의 향상은 Leaky ReLU와 SELU에서는 완벽히 살리지 못했다. 또한 대부분 연속적인 기울기 분포를 가지는 형태는 고려하지 않았다.
2017년 Google Brain 팀 소속 Prajit Ramachandran 외 2인의 논문 <SEARCHING FOR ACTIVATION FUNCTIONS> 에서 새로운 활성화 함수 Swish를 제안한다.
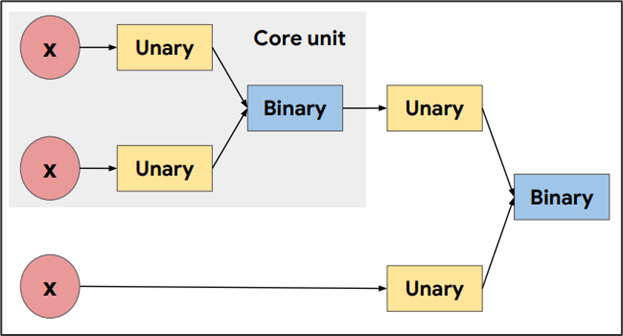

이 논문은 Unary 함수와 Binary 함수를 후보군으로 하는 RNN Controller (Zoph et al., 2017)을 적용하여 최적의 활성화 함수를 찾는 인상적인 실험을 진행하였다.
결과적으로 가장 우수한 성능을 보였던 함수, x * sigmoid(B*x)로 표현되는 Swish 함수는 다음과 같은 특징을 갖는다고 저자는 설명한다. 참고로 Swish는 계수 B(베타)를 제외하면 SiLU(Sigmoid Linear Unit, Elfwing et al., 2017)와 형태가 같다.
- 활성화 이전의 출력 x를 그대로 활용하는 함수들이 우수한 경향을 보임
- 단순한 형태; 복잡한 형태의 수식은 최적화를 더 어렵게 만든다.
- 비단조성 'bump'; 음의 활성화 값을 보전하되, 연속적인 기울기 변화를 갖는 구간
- ReLU 함수와 달리 양의 구간에서 일정한 기울기를 가지지 않음 (non-preserving gadient)
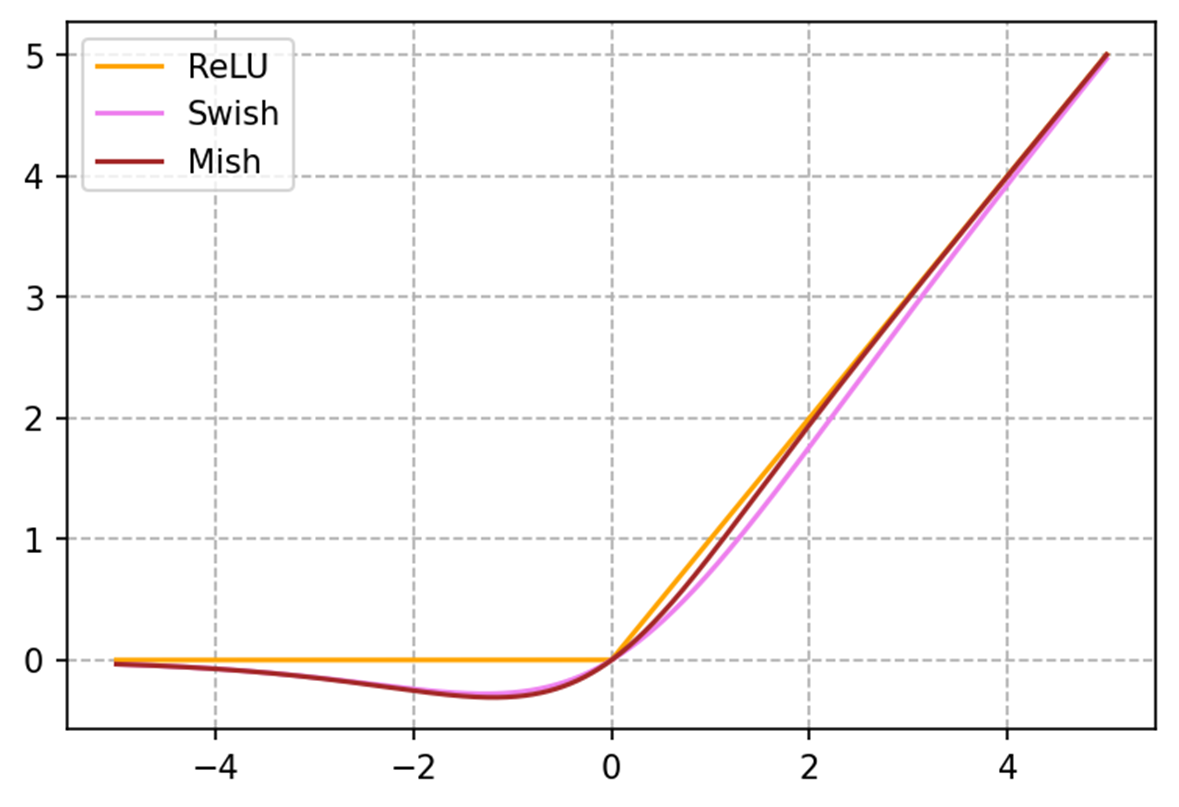
이어 2019년 Diganta Misra의 논문 <Mish: A Self Regularized Non-Monotonic Activation Function>에서 제안한 Mish (x ∗ tanh(ln(1+e^x))는 다음과 같은 특성을 갖는 것으로 저자는 설명한다.
- x < 0 구간에서 0으로 bounding되는 활성화 값; 연속적이고 smooth하면서 여전히 ReLU와 같은 강력한 정규화를 수행
- 전반적으로 smooth한 기울기 변화; 손실함수의 변화 역시 smooth해지면서 최적화에 긍정적인 효과
아쉬운 점은 실험적으로 Mish가 Swish보다 우수하다는 것을 증명했지만, 그것이 어떤 특성에서 기인한 것인지 밝힌 바는 앞서 살펴본 특성들과 크게 다르지 않다는 것이다.
Reference
https://paperswithcode.com/methods/category/activation-functions
Papers with Code - An Overview of Activation Functions
Activation functions are functions that we apply in neural networks after (typically) applying an affine transformation combining weights and input features. They are typically non-linear functions. The rectified linear unit, or ReLU, has been the most pop
paperswithcode.com
https://arxiv.org/abs/1710.05941v2
Searching for Activation Functions
The choice of activation functions in deep networks has a significant effect on the training dynamics and task performance. Currently, the most successful and widely-used activation function is the Rectified Linear Unit (ReLU). Although various hand-design
arxiv.org
https://arxiv.org/abs/1908.08681v3
Mish: A Self Regularized Non-Monotonic Activation Function
We propose $\textit{Mish}$, a novel self-regularized non-monotonic activation function which can be mathematically defined as: $f(x)=x\tanh(softplus(x))$. As activation functions play a crucial role in the performance and training dynamics in neural networ
arxiv.org
https://arxiv.org/abs/1611.01578
Neural Architecture Search with Reinforcement Learning
Neural networks are powerful and flexible models that work well for many difficult learning tasks in image, speech and natural language understanding. Despite their success, neural networks are still hard to design. In this paper, we use a recurrent networ
arxiv.org
https://www.sciencedirect.com/science/article/pii/S0925231222008426
Activation functions in deep learning: A comprehensive survey and benchmark
Neural networks have shown tremendous growth in recent years to solve numerous problems. Various types of neural networks have been introduced to deal…
www.sciencedirect.com
'Machine Learning > Deep Neural Network' 카테고리의 다른 글
| [StackExchange 펌] CNN 오버피팅 방지와 배치 사이즈 (0) | 2023.02.28 |
|---|---|
| [DL] Activation Functions Insight ~ Sigmoid, tanh, ReLU (0) | 2023.01.02 |
| 손실 함수(Cost / Loss Function) 정리 - MSE, CEE, RMSE, MAE (0) | 2022.11.15 |

