이 글에서는 활성화 함수 중 대표적인 것들을 살펴보고, 그 발전에 있던 insight들을 이해하며 활성화 함수의 역할과 이를 위한 특성을 이해해보려고 한다.
딥 러닝 모델에 있어 활성화 함수는 다음과 같은 역할을 가진다.
- 모델에게 주어진 문제를 분석하는 데에 있어 비선형성을 더해 더 정확하고 일반화된 가설을 세우도록 한다.

퍼셉트론에서 사용된 이진 분류용 step function을 보면 최초 활성화 함수의 역할이 어떤 것에 초점을 맞추고 있는지 알 수 있다.

최초의 활성화 함수는 이진 분류를 위해 0, 1의 출력으로 구분하여 활성화 값을 분류하는 것이었다.
하지만 뉴런 층을 깊게 하여 기계 스스로 복잡하고 비선형성을 띄는 문제를 해결하는 딥 러닝 이론이 연구되면서, 이러한 이진 활성화 함수는 딥 러닝 방법론의 알파, 경사하강법의 측면에서 문제를 맞게 된다.
step function을 통과하면서 활성화 값에 대한 기울기가 사라져 ((0, 0)에서 무한대, 이외 구간에서 0) 경사하강법을 진행할 수 없는 것이다.
이를 보완하기 위해 sigmoid 함수가 사용되게 된다.
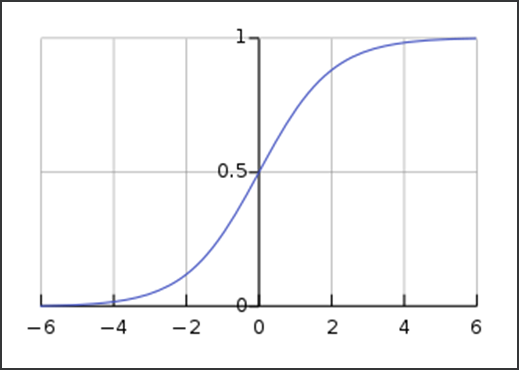
(이 분야에서는 sigmoid 함수로 으레 부르지만 이는 s자 형태의 모든 함수를 일컫는 말이고, 위 함수의 정확한 명칭은 logistic 함수이다.)
step function에 기울기를 적용한 형태로도 볼 수 있는 sigmoid 함수 = 1 / (1 + e^(-x))는 출력이 (0, 1) 범위로 제한되어 있다.
하지만 특정 값으로 수렴하는 출력은 기울기 값이 0으로 수렴하는 기울기 소실 문제로, 비교적 작은 기울기 값 분포는 학습 효율 감소라는 문제로 이어지게 된다.
또한 값이 수렴하는 주제에 양수의 범위에서만 값을 표현 가능하다는 점은 음의 활성화 값을 보전하지 못 하는 제약이 생기게 한다.
다만 LSTM의 gate 연산과 같이 특정 비율에 대한 연산이나, 이진 분류의 출력층 연산의 경우 0 ~ 1 사이의 값을 반환하는 점은 확률의 공리에 맞는 적절한 출력으로 생각되어 활용할 수 있을 것이다.

출력이 (-1, 1) 범위로 제한되어 있고 그에 따라 기울기 분포 값도 더 큰 tanh 함수(하이퍼볼릭 탄젠트) 역시 존재한다.
음의 값을 효과적으로 보전하고 학습 역시 더욱 잘 진행되지만 여전히 수렴 값에 가까워질수록 기울기가 0으로 수렴하여 학습이 진행이 되지 않는 문제가 있다.

다음은 ReLU (Rectified Linear Unit)의 사용이다.
tensorflow의 백엔드 연산으로 구현한다면 K.maximum(x, 0)이 되는데, (0, 0) 좌표를 기준으로 양의 구간에서는 활성화 값이 선형으로 반환되고, 음의 구간에서는 0.0으로 반환된다.
ReLU의 특성은 아래와 같이 정리할 수 있다.
- 예측에 의미가 적은 활성화 값의 범위를 음의 범위로 정의하고 이 값을 무시하도록 설계(강력한 정규화)
- 양의 구간은 선형적인 값을 반환해 unbounded하고 균일한 기울기 값을 가져, 앞선 활성화 함수들의 기울기 소실 문제를 해결. 값 자체는 무한대로 발산하지만 그 기울기는 일정하다는 점이 포인트.
즉, 활성화 값 기울기에 대한 이진분류로 이해할 수 있다. ReLU의 기울기 분포도는 step function이 된다.
- 이러한 음/양 구간의 개형 차이가 선형 활성화 함수와 달리 비선형성을 모델에 제공한다.
하지만 여전히 음의 구간에 들어서면 sigmoid, tanh 보다도 칼같은 기울기 삭제로 인해 dying neuron, 즉 활성화 값 부호가 음이 된 뉴런은 숨통이 끊기는 문제가 생긴다.
또한 불연속적인 기울기 분포는 dL/dW(가중치에 대한 손실함수 변화량) 에 대한 학습률 역시 불연속하게 만들어 안정적인 학습에 저해가 된다고 알려져 있다.
원래는 미분 불가능한 지점이 있으면 기울기가 존재하지 않는 점이 생겨 사용이 불가능하다고 알려져 있지만 경험적으로 보나 최근 활성화 함수 동향을 보나 그렇진 않다. 초기값에 예민하긴 하겠지만 값 자체가 급격하게 발산하지 않으면서 유의미한 값을 가지면 된다.
아무튼 이에 위 문제점을 해결하기 위한 여러 개선판이 등장하게 된다.
여기부터는 2부 글에서 다루도록 하겠다.
Reference
- Shiv Ram Dubey, Satish Kumar Singh, Bidyut Baran Chaudhuri, Activation functions in deep learning: A comprehensive survey and benchmark, Neurocomputing, Volume 503, 2022, Pages 92-108, ISSN 0925-2312.
Elsevier Enhanced Reader
To print this document, select the Print icon or use the keyboard shortcut, Ctrl + P.
reader.elsevier.com
- 사이토 고키, 밑바닥부터 시작하는 딥러닝, 한빛미디어.
- https://paperswithcode.com/method/tanh-activation
Papers with Code - Tanh Activation Explained
Tanh Activation is an activation function used for neural networks: $$f\left(x\right) = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}}$$ Historically, the tanh function became preferred over the sigmoid function as it gave better performance for multi-layer neural
paperswithcode.com
ReLU - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. ReLU 함수에 대한 그래프 ReLU 함수는 정류 선형 유닛(영어: Rectified Linear Unit 렉티파이드 리니어 유닛[*])에 대한 함수이다. ReLU는 입력값이 0보다 작으면 0으로 출
ko.wikipedia.org
https://ko.wikipedia.org/wiki/%EC%8B%9C%EA%B7%B8%EB%AA%A8%EC%9D%B4%EB%93%9C_%ED%95%A8%EC%88%98
시그모이드 함수 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 시그모이드 함수는 S자형 곡선 또는 시그모이드 곡선을 갖는 수학 함수이다. 시그모이드 함수의 예시로는 첫 번째 그림에 표시된 로지스틱 함수가 있으며 다음
ko.wikipedia.org
'Machine Learning > Deep Neural Network' 카테고리의 다른 글
| [StackExchange 펌] CNN 오버피팅 방지와 배치 사이즈 (0) | 2023.02.28 |
|---|---|
| [DL] Activation functions Insight ~ Swish와 Mish (0) | 2023.01.13 |
| 손실 함수(Cost / Loss Function) 정리 - MSE, CEE, RMSE, MAE (0) | 2022.11.15 |

